Oct 22, 2024. Jul 19, 2024

Here is a list of my current and past research projects, I hope you'll find something interesting!.

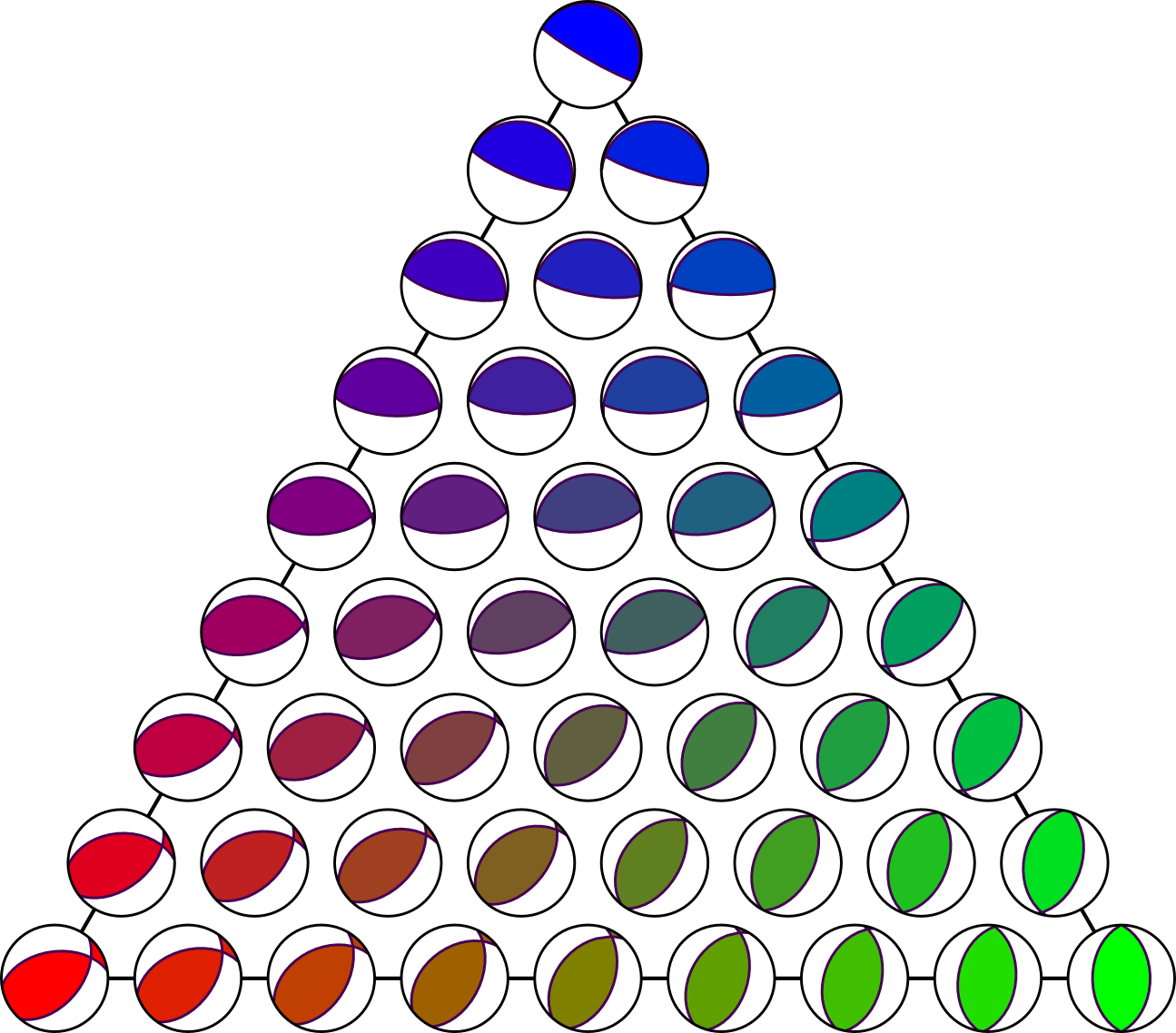
Sparse fault representation

I am developing a hybrid source representation that bridges the gap between conventional finite fault models and multiple-point sources used to represent large earthquake ruptures. Based on the geometrical properties of Moment Tensor sources, I have developed an interpolation scheme that allows the representation of a quasi-continuous slip distribution along a fault based on a set of key moment tensors.

This sparse representation benefits both the forward modeling and the inverse problem, as it allows for a compact representation of the parameters to be inverted while also providing a quasi-continuous representation of the slip distribution by interpolation.

Trilinear MT interpolation
Example of moment tensor interpolation applied to the three key tensors at the edges of the triangle (Red, Blue, and Green) in order to redistribute sources over space within the triangle.

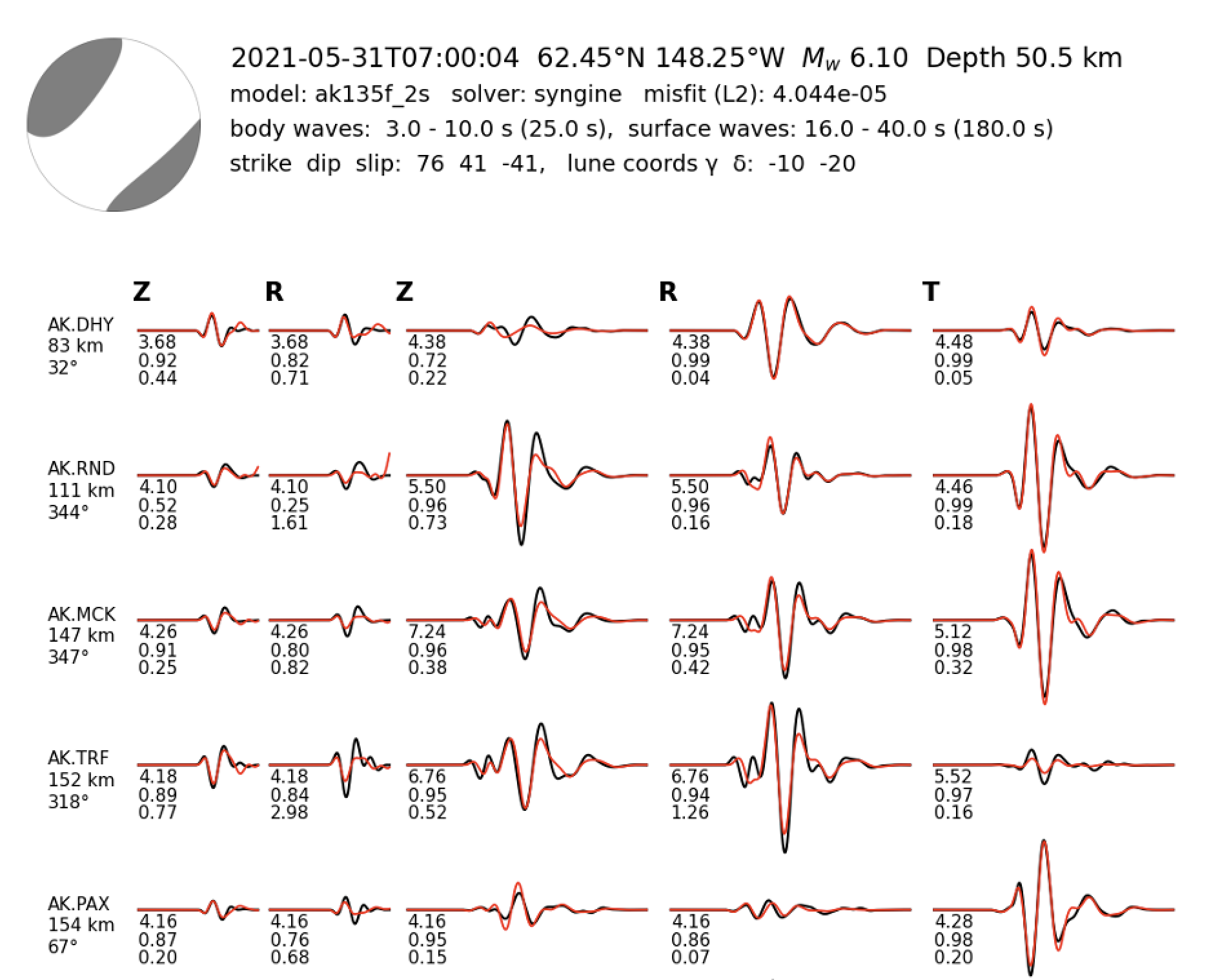
MTUQ

I am one of the lead developers of the MTUQ package, a Python-based software for Moment Tensor inversion and Uncertainty Quantification. MTUQ is designed to be a flexible (hackable design) and user-friendly tool for inverting seismic waveform and first motion polarity data.

MTUQ is based of the cut-and-paste method, and is designed to be adaptable to different research needs, offering customizable data processing and misfit functions as well as built-in support for commonly used solver output formats (SPECFEM3D, AxiSEM, FK). In addition, the package aims to be efficient enough for operational use cases, including applications to large event catalogs.

MTUQ
Example of waveform fit figure for a moment tensor solution generated with MTUQ.

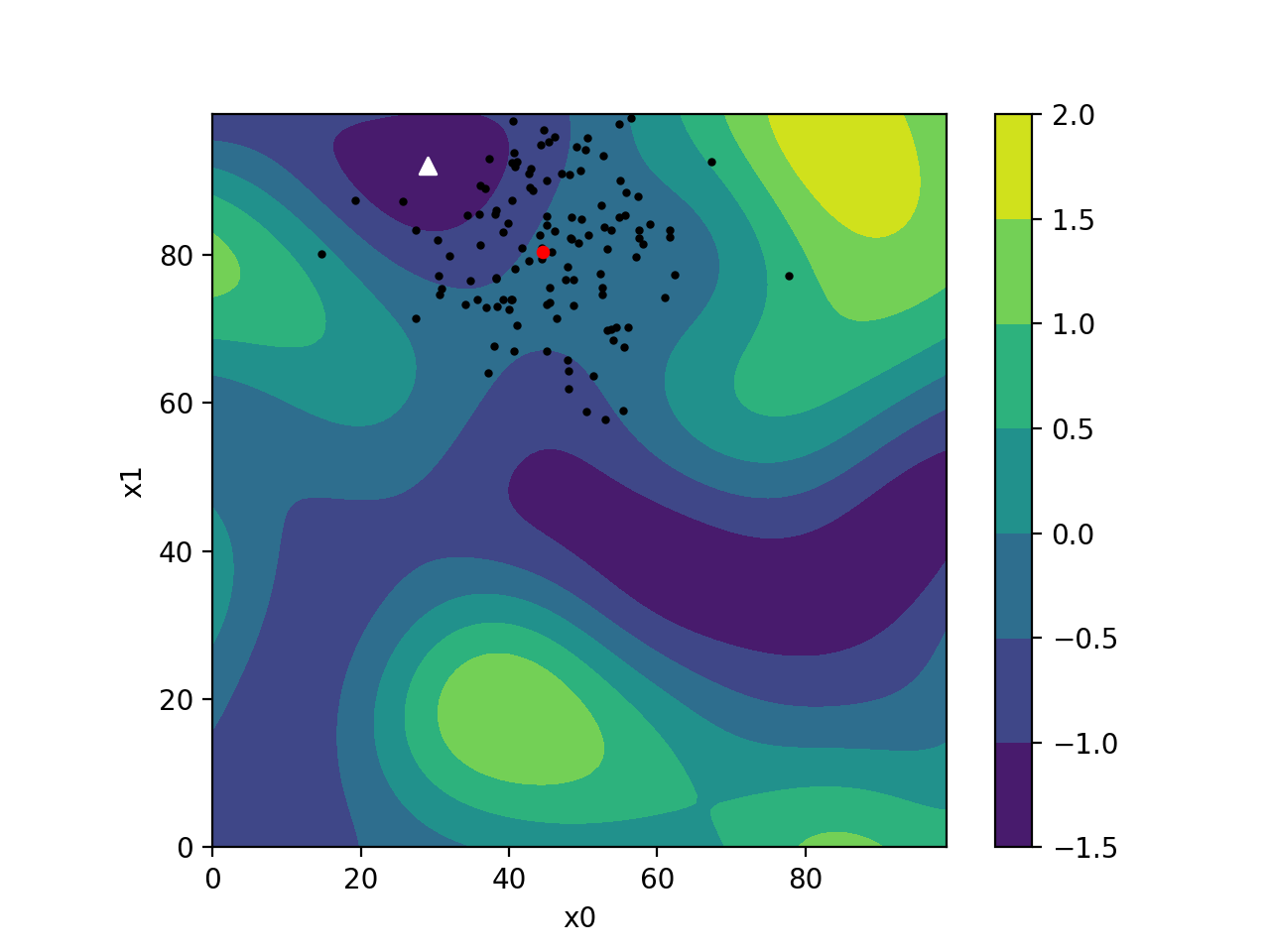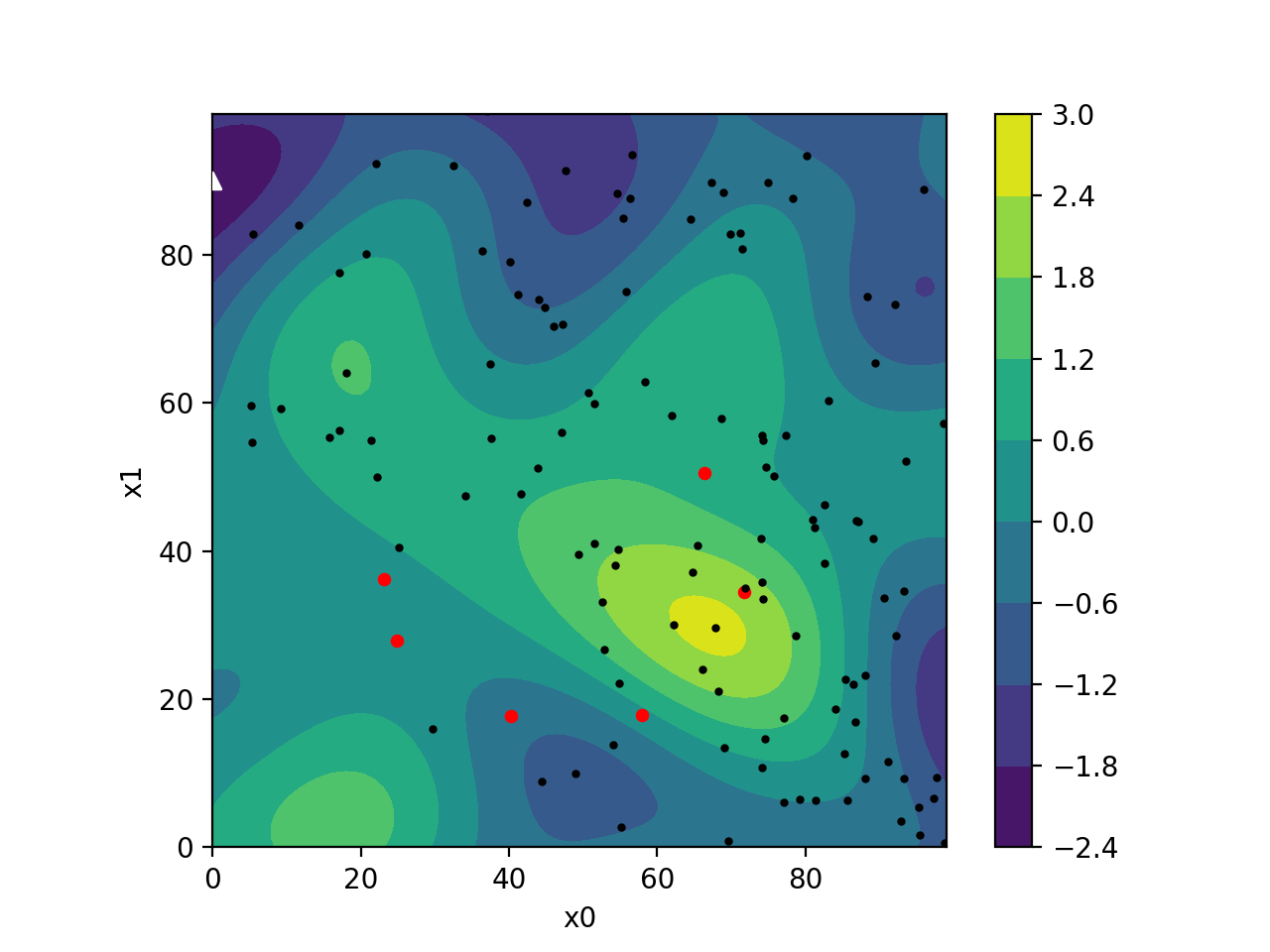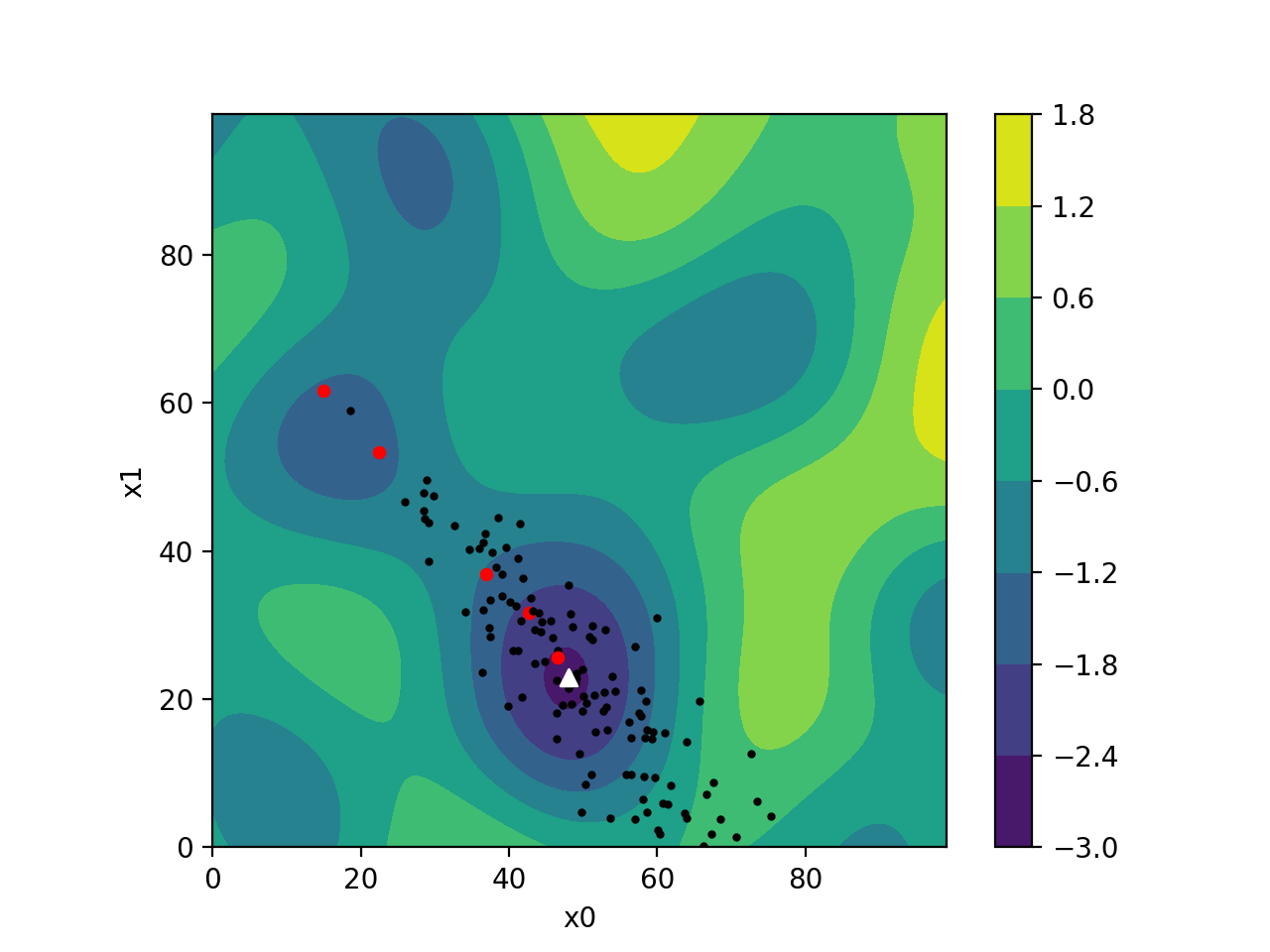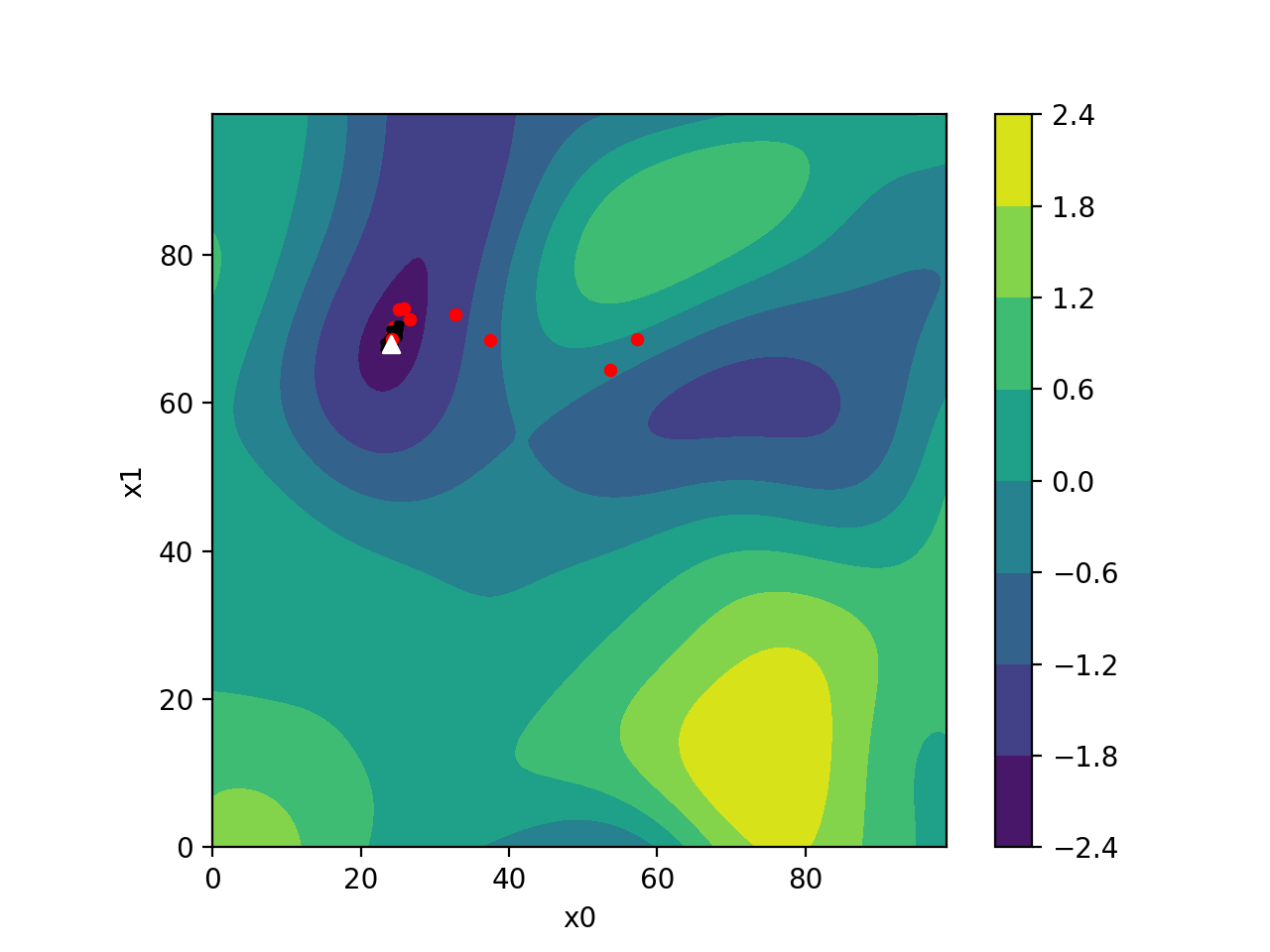
CMA-ES

I am exploring the use of black box optimization for the source inversion problem using the Covariance Matrix Adaptation Evolution Strategy (CMA-ES). CMA-ES is a self-adaptive, population-based optimization algorithm that has been shown to be efficient for low-dimensional optimization problems.

One of its main advantages is that it does not require the computation of gradients, making it particularly suitable for exploring various inverse problems and rapidly prototyping new source inversion methods. While it does not guarantee finding the global minimum, CMA-ES is generally efficient at avoiding local minima and has shown competitive results for global optimisation.

MTUQ
Visualization of the CMA-ES algorithm on 2D Gaussian random fields. The CMA-ES uses a population of mutants (black dots) to successively update the mean (red) and covariance of a search distribution, in order to find the minimum of the 2D function.

specfem_tomo_helper

In an attempt to simplify the use of external tomography models in SPECFEM3D, I have developed specfem_tomo_helper, a helper code designed to extract, prepare, and save a tomographic model in the correct format from NetCDF files obtained on the IRIS EMC library of models.

specfem_tomo_helper is written in Python and comes with a light graphical user interface to help select the area of interest within an existing model. It then automatically handles projection from geographical coordinates into cartesian coordinates, as well as regular grid interpolation. The code is still in an early stage of development but should be enough to get people started on simple use cases.

Tomographic model
Preview of a 3D tomographic file in UTM coordinates, extracted and resampled from an IRIS EMC NetCDF model.

Waveform modeling - source upsampling

As I work primarily with seismic waveform data, I am naturally interested in waveform modeling. I am exploring the use of source upsampling using moment tensor interpolation, in order to produce very smooth, high-resolution slip models, from coarse finite-fault solutions.

Thanks to this approach, it is possible to revisit any past earthquake from which we have a source model (USGS Finite Fault product), and make them compatible with 3D waveform simulation solver like SPECFEM3D or SPECFEM3D_Globe, without increasing the computational cost (the source model gets improved without impacting the modeling scheme).

Simulation (vertical displacement) of an upscaled source model for the 1964 Great Alaska earthquake. The original source model included 488 patches, which were upscaled to over 40,000 point sources to create this smooth simulation, thereby preventing any artifacts commonly associated with point sources.

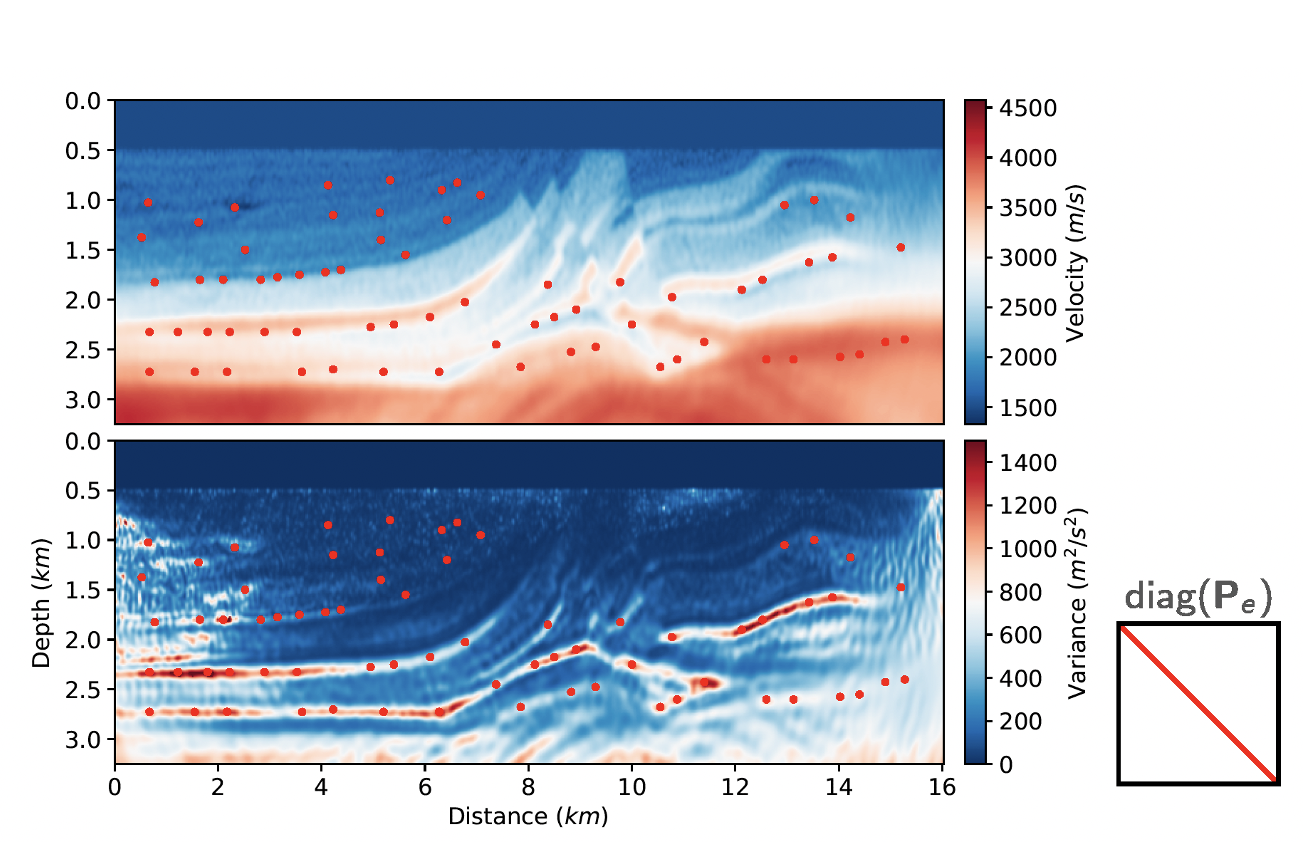
Uncertainty estimation in full waveform inversion

Taking cues from the Data assimilation and numerical weather forecasting communities, I have implemented an uncerainty estimation method for Full Waveform Inversion/Tomography, based on the Ensemble Kalman Filter called the ETKF-FWI. The goal of this method is to provide systematic uncertainty estimation, in a way that is computationally feasible (albeit still expensive), as part of the inversion itself, rather than being a post-processing procedure.

By treating the FWI as an non-linear operator that changes an initial Earth model, I showed it was possible to integrate it within an Ensemble Kalman filter, which allows propagating uncertainties through an ensemble of models, and approximate a low-rank version of the posterior covariance matrix.

Uncertainty estimation
ETKF-FWI inversion results on a 2D synthetic benchmark. The top panel represents the mean of an ensemble of models, and the bottom represents the variance map (diagonal of the ensemble covariance matrix), which translates to how much agreement there is amongst the ensemble members for each point in the subsurface. High variance values typically indicate low convergence and high uncertainty. The red dots are co-registered local variance maxima, and are typically found at hard-to-recover interfaces.